Machine Learning Project: Building Deep Neural Network

Building Deep Neural Network

1 - Packages

import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases_v4 import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

2 - Outline

To implement our deep neural network, we will introduce some helper functions.

• Initialize the parameters for a two-layer network and for an L-layer neural network.
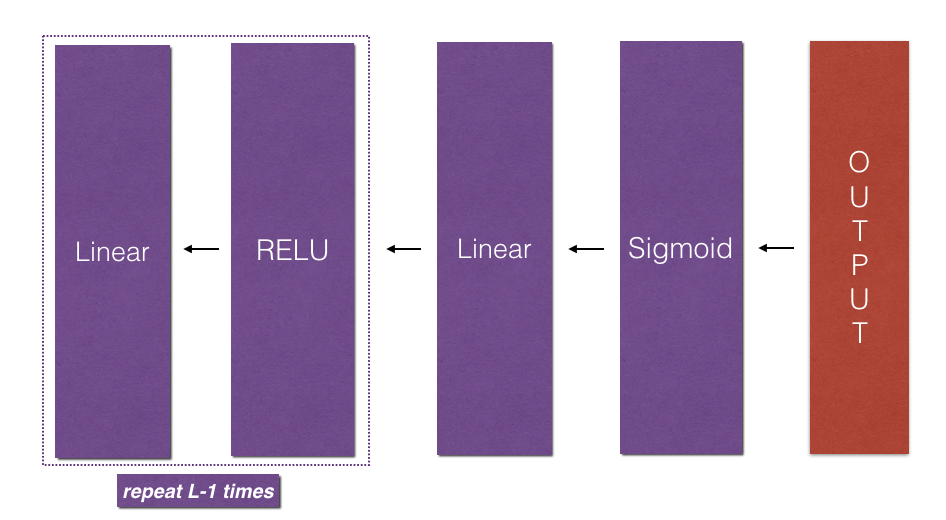
• Implement the forward propagation module (shown in purple in the figure below).
  • Complete the LINEAR part of a layer’s forward propagation step (resulting in Z[l] ).
  • We give you the ACTIVATION function (relu/sigmoid).
  • Combine the previous two steps into a new [LINEAR->ACTIVATION] forward function.
  • Stack the [LINEAR->RELU] forward function L-1 time (for layers 1 through L-1) and add a [LINEAR->SIGMOID] at the end (for the final layer L). This gives you a new L_model_forward function.
• Compute the loss.
• Implement the backward propagation module (denoted in red in the figure below).
  • Complete the LINEAR part of a layer’s backward propagation step.
  • We give you the gradient of the ACTIVATE function (relu_backward/sigmoid_backward)
  • Combine the previous two steps into a new [LINEAR->ACTIVATION] backward function.
  • Stack [LINEAR->RELU] backward L-1 times and add [LINEAR->SIGMOID] backward in a new L_model_backward function
• Finally update the parameters.

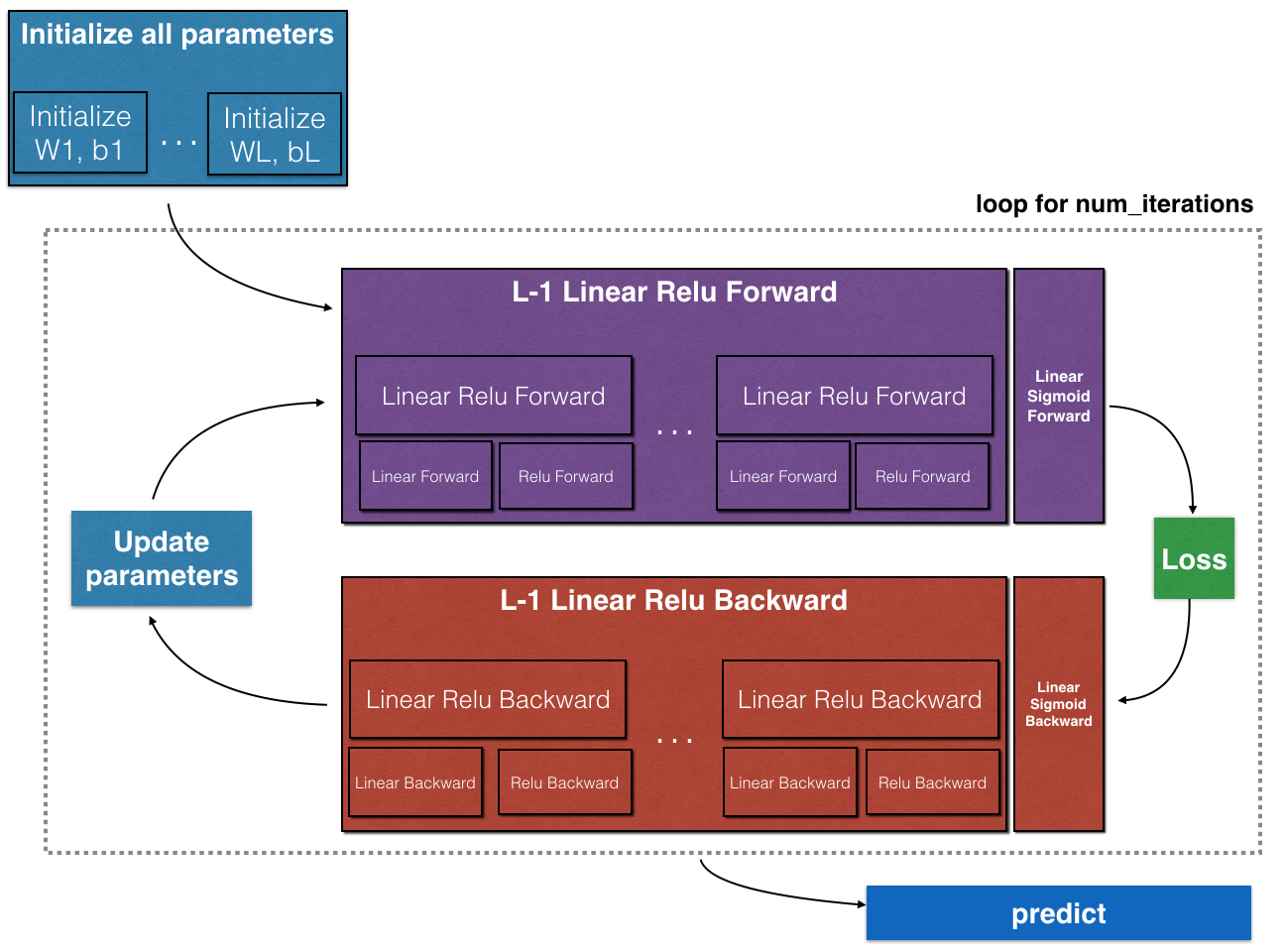
Note that for every forward function, there is a corresponding backward function. That is why at every step of your forward module you will be storing some values in a cache. The cached values are useful for computing gradients. In the backpropagation module you will then use the cache to calculate the gradients.

Initialization

• The model’s structure is [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID. I.e., it has L−1 layers using a ReLU activation function followed by an output layer with a sigmoid activation function.
• We use random initialization for the weight matrices. ex. np.random.randn(shape) * 0.01.
• We use zeros initialization for the biases. ex. np.zeros(shape). We will store n[l] , the number of units in different layers, in a variable layer_dims. For example, the layer_dims for the “Planar Data classification model” would have been [2,4,1]: There were two inputs, one hidden layer with 4 hidden units, and an output layer with 1 output unit. Thus means W1’s shape was (4,2), b1 was (4,1), W2 was (1,4) and b2 was (1,1). Now we will generalize this to L layers.

def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the dimensions of each layer in our network

    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    bl -- bias vector of shape (layer_dims[l], 1)
    """

    np.random.seed(3)
    parameters = {}
    L = len(layer_dims)            # number of layers in the network

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])*0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l],1))

        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))


    return parameters

Forward Propagation Module

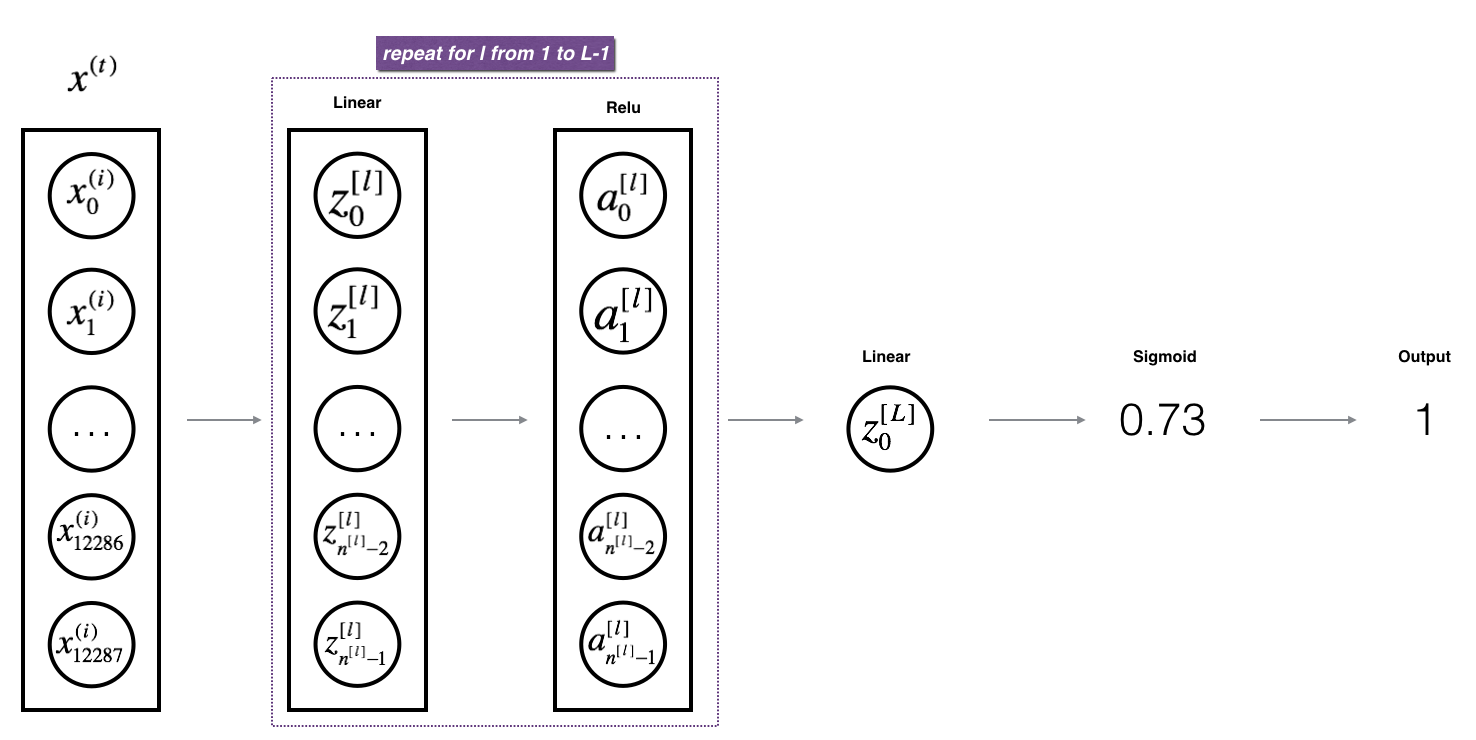
def linear_activation_forward(A_prev, W, b, activation):
    """
    Implement the forward propagation for the LINEAR->ACTIVATION layer

    Arguments:
    A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"

    Returns:
    A -- the output of the activation function, also called the post-activation value
    cache -- a python dictionary containing "linear_cache" and "activation_cache";
             stored for computing the backward pass efficiently
    """

    if activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)

    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)

    assert (A.shape == (W.shape[0], A_prev.shape[1]))
    cache = (linear_cache, activation_cache)

    return A, cache

def L_model_forward(X, parameters):
    """
    Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation

    Arguments:
    X -- data, numpy array of shape (input size, number of examples)
    parameters -- output of initialize_parameters_deep()

    Returns:
    AL -- last post-activation value
    caches -- list of caches containing:
                every cache of linear_activation_forward() (there are L-1 of them, indexed from 0 to L-1)
    """

    caches = []
    A = X
    L = len(parameters) // 2                  # number of layers in the neural network

    # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
    for l in range(1, L):
        A_prev = A
        A, cache = linear_activation_forward(A_prev,parameters["W"+str(l)],parameters["b"+str(l)],"relu")
        caches.append(cache)

    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    AL, cache = linear_activation_forward(A,parameters["W"+str(L)],parameters["b"+str(L)],"sigmoid")
    caches.append(cache)

    assert(AL.shape == (1,X.shape[1]))

    return AL, caches

Cost Function

Now we will implement forward and backward propagation. We need to compute the cost, because we want to check if our model is actually learning.

def compute_cost(AL, Y):
    """
    Implement the cost function defined by equation (7).

    Arguments:
    AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
    Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)

    Returns:
    cost -- cross-entropy cost
    """

    m = Y.shape[1]

    # Compute loss from aL and y.
    cost = -1/m*np.sum(np.multiply(np.log(AL),Y)+np.multiply(np.log(1-AL),1-Y))

    cost = np.squeeze(cost)      # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
    assert(cost.shape == ())

    return cost

Backward Propagation

Just like with forward propagation, we will implement helper functions for backpropagation. Remember that back propagation is used to calculate the gradient of the loss function with respect to the parameters.

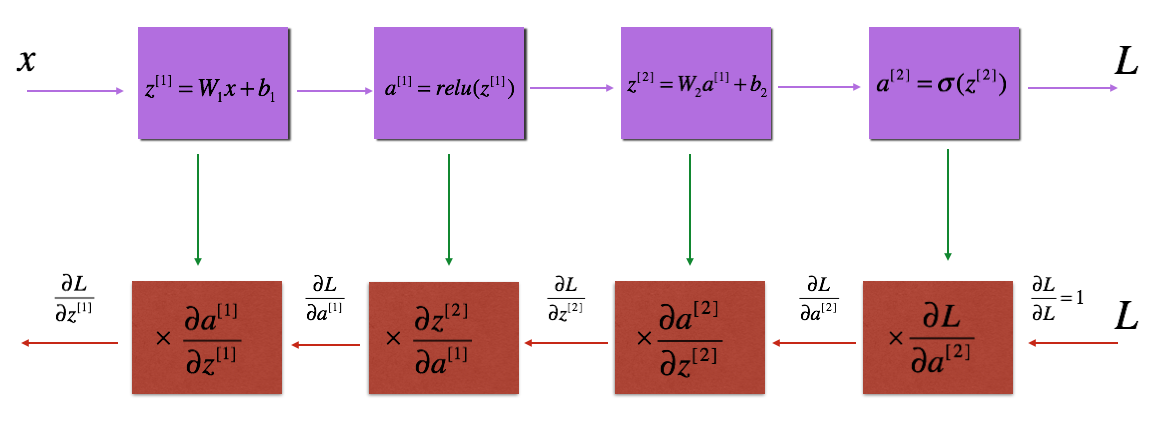
Now, similar to forward propagation, we are going to build the backward propagation in three steps:

1. LINEAR backward
2. LINEAR -> ACTIVATION backward where ACTIVATION computes the derivative of either the ReLU or sigmoid activation
3. [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID backward (whole model)

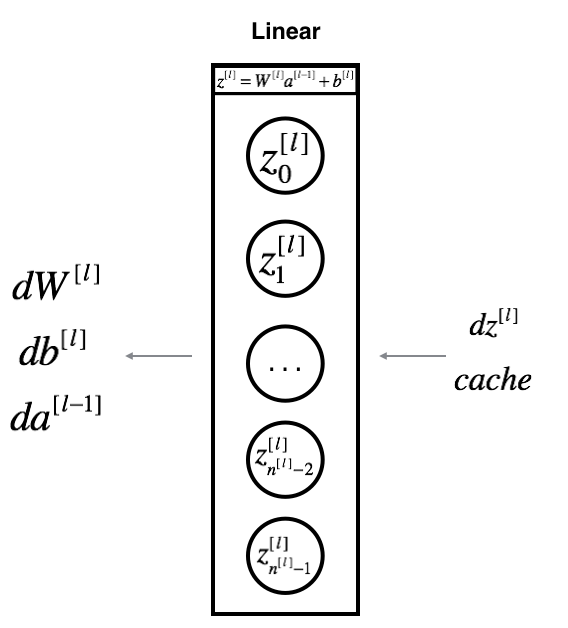
def linear_backward(dZ, cache):
    """
    Implement the linear portion of backward propagation for a single layer (layer l)

    Arguments:
    dZ -- Gradient of the cost with respect to the linear output (of current layer l)
    cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer

    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW -- Gradient of the cost with respect to W (current layer l), same shape as W
    db -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = 1/m*np.dot(dZ,A_prev.T)
    db = np.sum(dZ,axis=1,keepdims=True)/m
    dA_prev = np.dot(W.T,dZ)

    assert (dA_prev.shape == A_prev.shape)
    assert (dW.shape == W.shape)
    assert (db.shape == b.shape)

    return dA_prev, dW, db

Next, we will create a function that merges the two helper functions: linear_backward and the backward step for the activation linear_activation_backward.

def linear_activation_backward(dA, cache, activation):
    """
    Implement the backward propagation for the LINEAR->ACTIVATION layer.

    Arguments:
    dA -- post-activation gradient for current layer l
    cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"

    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW -- Gradient of the cost with respect to W (current layer l), same shape as W
    db -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    linear_cache, activation_cache = cache

    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)

    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)

    return dA_prev, dW, db

Now we will implement the backward function for the whole network. Recall that when we implemented the L_model_forward function, at each iteration, we stored a cache which contains (X,W,b, and z). In the back propagation module, we will use those variables to compute the gradients. Therefore, in the L_model_backward function, we will iterate through all the hidden layers backward, starting from layer L . On each step, we will use the cached values for layer l to backpropagate through layer l . Figure below shows the backward pass.

def L_model_backward(AL, Y, caches):
    """
    Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group

    Arguments:
    AL -- probability vector, output of the forward propagation (L_model_forward())
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
    caches -- list of caches containing:
                every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
                the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])

    Returns:
    grads -- A dictionary with the gradients
             grads["dA" + str(l)] = ...
             grads["dW" + str(l)] = ...
             grads["db" + str(l)] = ...
    """
    grads = {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL

    # Initializing the backpropagation
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

    # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "dAL, current_cache". Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"]
    current_cache = linear_activation_backward(dAL, caches[L-1], "sigmoid")
    grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = current_cache

    # Loop from l=L-2 to l=0
    for l in reversed(range(L-1)):
        # lth layer: (RELU -> LINEAR) gradients.
        # Inputs: "grads["dA" + str(l + 1)], current_cache". Outputs: "grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]

        current_cache = linear_activation_backward(grads["dA" + str(l + 1)], caches[l],"relu")
        dA_prev_temp, dW_temp, db_temp = current_cache
        grads["dA" + str(l)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp

    return grads

Update Parameters

def update_parameters(parameters, grads, learning_rate):
    """
    Update parameters using gradient descent

    Arguments:
    parameters -- python dictionary containing your parameters
    grads -- python dictionary containing your gradients, output of L_model_backward

    Returns:
    parameters -- python dictionary containing your updated parameters
                  parameters["W" + str(l)] = ...
                  parameters["b" + str(l)] = ...
    """

    L = len(parameters) // 2 # number of layers in the neural network

    # Update rule for each parameter. Use a for loop.
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)]-learning_rate*grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)]-learning_rate*grads["db" + str(l+1)]
    return parameters

Model

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):#lr was 0.009
    """
    Implements a L-layer neural network: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.

    Arguments:
    X -- data, numpy array of shape (number of examples, num_px * num_px * 3)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
    layers_dims -- list containing the input size and each layer size, of length (number of layers + 1).
    learning_rate -- learning rate of the gradient descent update rule
    num_iterations -- number of iterations of the optimization loop
    print_cost -- if True, it prints the cost every 100 steps

    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    np.random.seed(1)
    costs = []                         # keep track of cost

    # Parameters initialization. (≈ 1 line of code)
    parameters = initialize_parameters_deep(layers_dims)

    # Loop (gradient descent)
    for i in range(0, num_iterations):

        # Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
        AL, caches = L_model_forward(X, parameters)

        # Compute cost.
        cost = compute_cost(AL, Y)

        # Backward propagation.
        grads = L_model_backward(AL, Y, caches)

        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)


        # Print the cost every 100 training example
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)

    # plot the cost
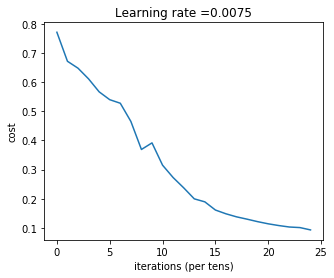
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()

    return parameters

Test the model with a dataset

Again we have a data such that:

• a training set of m_train images labelled as cat (1) or non-cat (0)
• a test set of m_test images labelled as cat and non-cat
• each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB).

train_x_orig, train_y, test_x_orig, test_y, classes = load_data()

# Reshape the training and test examples
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T   # The "-1" makes reshape flatten the remaining dimensions
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T

# Standardize data to have feature values between 0 and 1.
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.

print ("train_x's shape: " + str(train_x.shape))
print ("test_x's shape: " + str(test_x.shape))

train_x’s shape: (12288, 209) test_x’s shape: (12288, 50)

Note that 12,288 equals 64×64×3 which is the size of one reshaped image vector.

General Methodology:

1. Initialize parameters / Define hyperparameters
2. Loop for num_iterations: a. Forward propagation b. Compute cost function c. Backward propagation d. Update parameters (using parameters, and grads from backprop)
3. Use trained parameters to predict labels

parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)

• Cost after iteration 0: 0.771749
• Cost after iteration 100: 0.672053
• Cost after iteration 200: 0.648263
• Cost after iteration 300: 0.611507
• Cost after iteration 400: 0.567047
• Cost after iteration 500: 0.540138
• Cost after iteration 600: 0.527930
• Cost after iteration 700: 0.465477
• Cost after iteration 800: 0.369126
• Cost after iteration 900: 0.391747
• Cost after iteration 1000: 0.315187
• Cost after iteration 1100: 0.272700
• Cost after iteration 1200: 0.237419
• Cost after iteration 1300: 0.199601
• Cost after iteration 1400: 0.189263
• Cost after iteration 1500: 0.161189
• Cost after iteration 1600: 0.148214
• Cost after iteration 1700: 0.137775
• Cost after iteration 1800: 0.129740
• Cost after iteration 1900: 0.121225
• Cost after iteration 2000: 0.113821
• Cost after iteration 2100: 0.107839
• Cost after iteration 2200: 0.102855
• Cost after iteration 2300: 0.100897
• Cost after iteration 2400: 0.092878

pred_train = predict(train_x, train_y, parameters)

Accuracy: 0.985645933014

pred_test = predict(test_x, test_y, parameters)

Accuracy: 0.8